This document provides basic statistics about the topology of the Web Data Commons - Hyperlink Graph extracted from the Common Crawl Corpus released in April 2014, covering 1.7 billion web pages and 64 billion hyperlinks between these pages. The graph was extracted from the Spring 2014 web corpus of the Common Crawl Foundation. This corpus was gathered using a modified Apache Nutch crawler to gather pages from a seed list without discovering links while crawling. The seed list,containing around 6 billion URLs was provided by the search engine company blekko where the crawl corpus contains around 2 billion of those pages. The Common Crawl Foundation and blekko started a cooperation in 2013 to increase the quality and popularity of the crawled pages and reduce the number of crawled spam pages and crawler traps. The graph of 2014 is well connected (91% of all nodes) the largest strongly connected component consists of only 19% of all nodes, which is most like due to the selected crawling strategy. Nevertheless we encourage the usage of this graph datasets but for analysis of the connectivity of the pages within the web and structural studies we recommend to use the 2012 graph dataset, as a BFS based selection strategy including link discovery while crawling most likely results in a more realistic sample of the structure of the Web.
Contents
1. Page Graph
This graph contains of over 1.7 billion nodes which are connected by over 64 billion arcs which are retrieved from the extracted hyperlinks of a crawled page. In the following we present the analysis of the degree and the components of the graph as well as the sizes of the bow-tie components, which can be found within the graph and was first introduced in the work Graph structure in the web by Broder et al. in 2000.
1.1 Indegree and Outdegree Distribution
The following two figures show frequency plots of indegrees
and outdegrees in log-log scale. For each d, we plot a point with
an ordinate equal to the number of pages with that have degree d. Note that
we included the data for degree zero, which is omitted in most of the
literature. We then aggregate the values using Fibonacci
binning to show the approximate shape of the distribution.
We find the page with the highest indegree to be referenced by of 45 million other pages and
the page with the largest number of links to contain almost 32 thousand references to other pages.
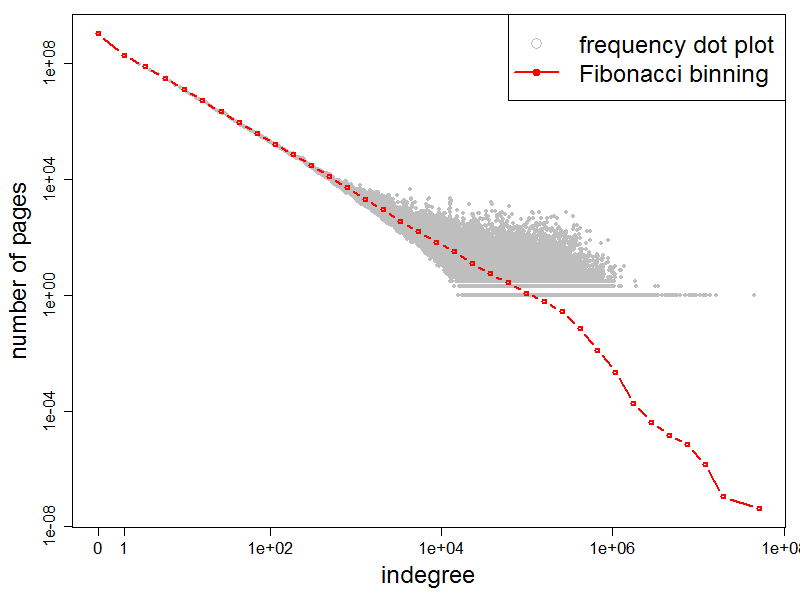 Frequency plot of the indegree distribution |
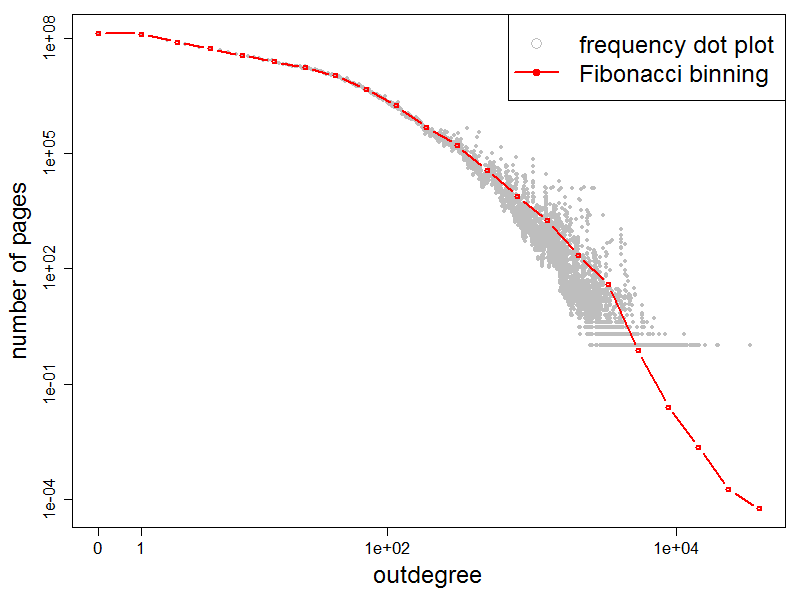 Frequency plot of the outdegree distribution |
1.2 Connected Components
The following figure (left) shows the distribution of the sizes of the
weakly connected components using a visualization similar to the previous
figures. The largest component (rightmost grey point) contains about around 91% of
the whole graph (over 1.54 billion pages).
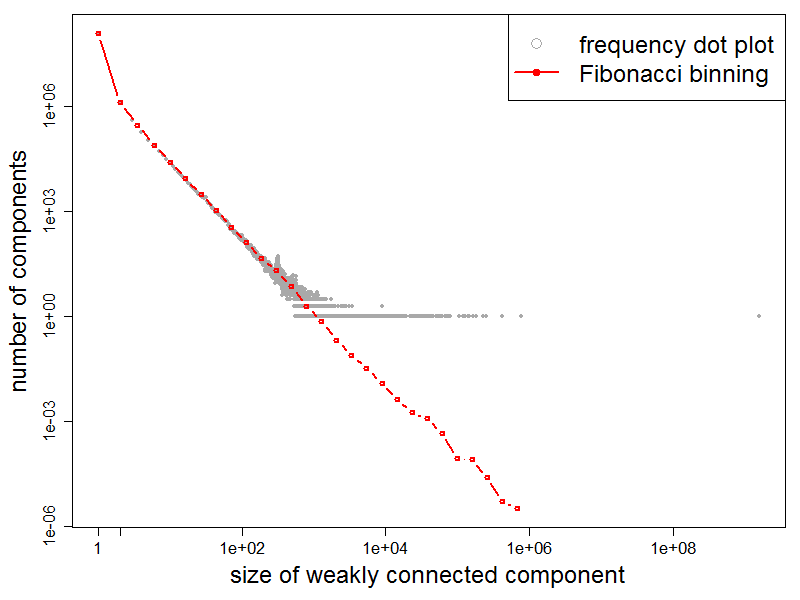
Frequency plot of the distribution of WCCs
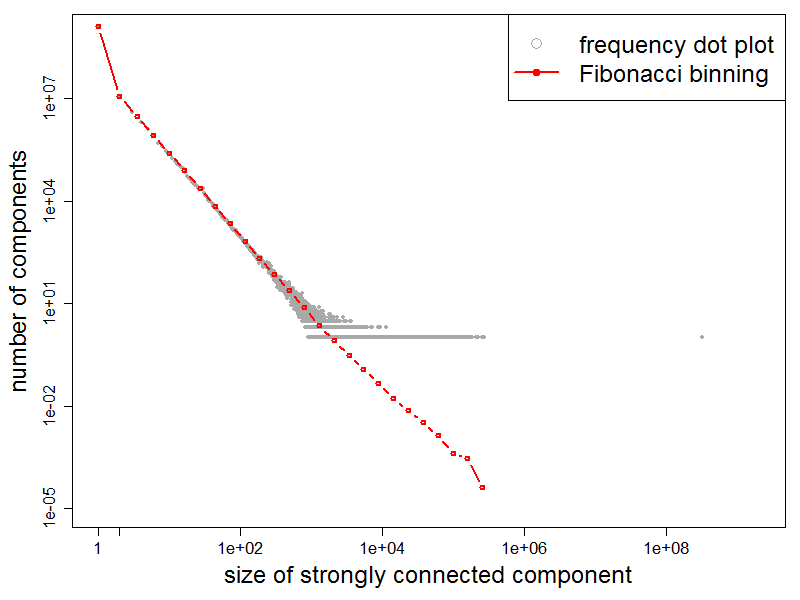
Frequency plot of the distribution of SCCs
1.3 Bow-Tie Structure
Having identified the giant strongly connected component, we can determine the so-called bow tie, a depiction of the structure of the web suggested by Broder et al.. The bow tie is made of six different components:
- the core is given by the giant strongly connected component (LSCC);
- the IN component contains non-core pages that can reach the core via a directed path;
- the OUT component contains non-core pages that can be reached from the core;
- the TUBES are formed by non-core pages reachable from IN and that can reach OUT;
- pages reachable from IN, or that can reach OUT, but are not listed above, are called TENDRILS;
- the remaining pages are DISCONNECTED.
x to y if some node in the
component associated with x is connected with a node in the component associated with y.
The bow tie of the page graph is shown in the following figure:

Bow-Tie Structure of the Page Graph
2. Credits
Lots of thanks to
- the Common Crawl project for providing their great web crawl and thus enabling the creation of the WDC Hyperlink Graph.
- Sebastiano Vigna for providing and supporting us with his amazing Java WebGraph library.
The creation of the WDC Hyperlink Graph was supported by the EU research project PlanetData and by Amazon Web Services through a Machine Learning Research Grant. We thank your sponsors a lot for supporting Web Data Commons.


